About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Phisics and Mathematics
The theory of the differential equations with the deviating argument belongs to number of the relatively young and roughly developing sections of the theory of the ordinary differential equations. There is a number of monographs, entirely or partially devoted to various aspects of this theory. We will specify, first of all, Myshkis A.D. monographs. [1], Elsgoltsa L.E. [2; 3], Krasovsky N. N. [4], Pinni E. [5], Bellman R. and Cook K.L. [6], Norkina of Page B. [7]. The equations with the late argument appear, for example, every time when in the considered physical or technical task force operating on a material point depends on speed or the provision of this point not only at present, but also at some moment preceding this.
For the equation with the deviating argument the considerable number of mathematical works is devoted to creation of the theory of boundary tasks in recent years. Now one of the directions in this theory is developed by Azbelevy N. V. and its pupils [14].
Problem
definition. Let ![]() - the square limited to pieces:
- the square limited to pieces:
![]()
Through
![]()
![]() we will designate a set of functions
we will designate a set of functions ![]() twice continuously differentiable on
twice continuously differentiable on ![]() and once continuously differentiable on
and once continuously differentiable on ![]() in area
in area ![]() . The border of area
. The border of area ![]() is understood as set of pieces
is understood as set of pieces ![]()
We will
consider in Hilbert space ![]() the mixed task for the heat conductivity equation:
the mixed task for the heat conductivity equation:
|
|
(1) (2) (3) |
where ![]()
To find Fourier decomposition of the solution of the mixed task (1)-(3).
The purpose - to receive Fourier submissions of solutions of a task (1)-(3).
II. MATERIAL AND METHODS
The regular solution of a task (1)-(3) we will
call the function ![]() turning
into identity the equation (1) and regional conditions (2)-(3).
turning
into identity the equation (1) and regional conditions (2)-(3).
We will
call function ![]() the strong solution of a task if there is a
sequence of functions
the strong solution of a task if there is a
sequence of functions ![]() and
meeting regional statements of the problem such
and
meeting regional statements of the problem such ![]() and
and ![]() , as meets in
, as meets in ![]() respectively
to
respectively
to ![]() and
and ![]() at
at ![]() .
.
The
regional task (1)-(3) is called strongly
solvable if the strong solution of a task exists for any right part ![]() and
only.[1-5]
and
only.[1-5]
In work methods of the complex analysis, theory of operators, theories of the differential equations, the spectral theory of differential operators and the theory of regular expansions are used.
III. RESULTS
Through
![]() we will
designate the operator determined by a formula
we will
designate the operator determined by a formula
![]()
In
space ![]() , it is obvious that
, it is obvious that ![]() the self-conjugate and unitary operator meeting a condition
the self-conjugate and unitary operator meeting a condition ![]() , where
, where ![]() - the single operator.
- the single operator.
Affecting
with the operator ![]() both members of equation (1), we have
both members of equation (1), we have
![]() .
.
Now we
investigate spectral properties of the operator ![]() . For this purpose we will consider a spectral task:
. For this purpose we will consider a spectral task:
|
|
(4) |
We look for the solution of this task in a look:
![]() .
.
Having substituted this expression in the equation (4), we will receive
![]() ,
,
![]() ,
,
![]() .
.
Therefore,
![]() ,
,
![]() .
.
from
where ![]() and
and ![]() .
.
For
functions ![]() we will
receive an infinite series of spectral tasks:
we will
receive an infinite series of spectral tasks:
![]()
![]() .
.
Thus,
at everyone fixed values ![]() it is
necessary to solve a spectral problem:
it is
necessary to solve a spectral problem:
|
|
(5) |
We will consider more general task:
|
|
(6) |
where ![]() - any complex (generally speaking) constant, and
- any complex (generally speaking) constant, and ![]() spectral
parameter.
spectral
parameter.
Having differentiated the equation and having used a boundary condition (6), we will receive a problem of Storm-Liouville:
![]() ,
,
![]()
![]()
![]()
![]()
![]()
If
function ![]() is own
function of a regional task (6), it is also own function for a problem of
Storm-Liouville:
is own
function of a regional task (6), it is also own function for a problem of
Storm-Liouville:
|
|
(7) (8) (9) |
Now we
will assume the return, i.e. let function ![]() be own function of a problem of Storm-Liouville (7)-(9), then
whether there will be it own function for a task (6)?
be own function of a problem of Storm-Liouville (7)-(9), then
whether there will be it own function for a task (6)?
We will find own functions of a regional task (7)-(9). From the equation (7) we have
![]()
Believing
![]() , we will receive
, we will receive
![]()
which common decision has an appearance:
![]()
where ![]() - any constants. Having substituted this expression
in boundary conditions (8)-(9), we have
- any constants. Having substituted this expression
in boundary conditions (8)-(9), we have
![]()
![]()
![]() ,
,
![]()
Therefore,
![]() .
.
As,
that ![]() , then
, then ![]() , i.e. own values of a regional task
, i.e. own values of a regional task
![]()
are squares of roots of the equation:
![]() ,
,
and own functions have an appearance:
![]() .
.
Having substituted this expression in the equation (7), we have
![]() .
.
Having
reduced by ![]() both
parts of equality, we have
both
parts of equality, we have
![]() .
.
We will transform the right part of this equality:
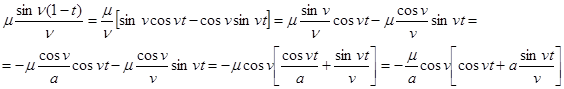
Therefore,
![]() ,
,
from where
![]() ,
,
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
,
![]() .
.
Thus,
if function ![]() is own
function of a problem of Storm Liouville (7)-(9), it is own function of also
regional task (6), where
is own
function of a problem of Storm Liouville (7)-(9), it is own function of also
regional task (6), where
![]() ,
, ![]() .
.
We proved the following lemma.
Lemma 1
Function ![]() is own
function of a regional task (6) in only case when it is own function of a
regional problem of Storm-Liouville (7)-(9).
is own
function of a regional task (6) in only case when it is own function of a
regional problem of Storm-Liouville (7)-(9).
If ![]() the
material size, a regional task (6) is self-conjugate therefore the problem of
Storm-Liouville also is self-conjugate and therefore has no the attached
functions, so rated own functions of a regional task (6) form orthonormalized
basis of space
the
material size, a regional task (6) is self-conjugate therefore the problem of
Storm-Liouville also is self-conjugate and therefore has no the attached
functions, so rated own functions of a regional task (6) form orthonormalized
basis of space ![]() .
.
Lemma 2 If ![]() the material constant, rated own functions of a
regional task (6) form orthonormalized basis of space
the material constant, rated own functions of a
regional task (6) form orthonormalized basis of space ![]() .
.
We will
designate own values of a regional task (5) through ![]() , and own functions corresponding to them through
, and own functions corresponding to them through ![]()
![]() , and own functions of a regional task (4) through
, and own functions of a regional task (4) through ![]() , then equality takes place:
, then equality takes place:
![]()
Lemma 3 Rated own functions of a regional task:
|
|
(10) (11) |
form
orthonormalized basis of space ![]() .
.
Proof.
Orthogonality of own functions of a regional task (10)-(11) follows from
symmetry of the operator ![]() therefore
it is enough to prove completeness of system
therefore
it is enough to prove completeness of system ![]()
![]() of own functions.
of own functions.
Let at
some functions ![]() equality
take place:
equality
take place:
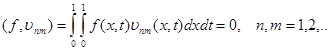
Then owing to Fubini's theorem it is had
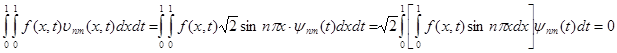
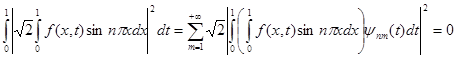
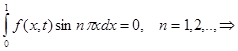
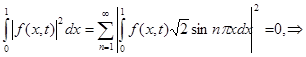
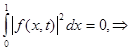
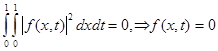
almost
everywhere in area ![]() , as was to be shown.
, as was to be shown.
In our
case ![]() and
and ![]() , therefore we can formulate the following
lemma.
, therefore we can formulate the following
lemma.
Lemma 4 Regional task (5) has an infinite set of own values:
![]()
where ![]() - roots of the equations
- roots of the equations
|
|
(12) |
and corresponding to them own functions
![]()
where ![]() - rated coefficients, and
- rated coefficients, and ![]() .
.
We will
assume that ![]() , then
, then ![]() also equality takes place:
also equality takes place:
![]() ,
,
where ![]() .
Therefore,
.
Therefore,
![]() .
.
Then
![]()
i.e.
the operator ![]() we will
turn. We will find the return operator
we will
turn. We will find the return operator ![]() .
.
![]()
As ![]() , that of the last equality follows quite the
operator's continuity
, that of the last equality follows quite the
operator's continuity ![]() .
.
Now we will return to our initial task. The solution of our task has an appearance:
![]()
where
![]()
![]()
![]()
![]() - roots of the equations (12),
- roots of the equations (12), ![]() - normalizing coefficients.
- normalizing coefficients.
IV. CONCLUSIONS
As a result of research the following theorem is proved.
Theorem
(a) The
mixed task (1)-(3) for the equation of heat conductivity is strongly solvable
in space ![]() ;
;
(b) The
return operator ![]() is
quite continuous on this space and Voltaire;
is
quite continuous on this space and Voltaire;
(c) "Spectral" decomposition takes place:
![]()
where ![]()
![]() ,
,
![]()
![]()
![]() - roots of the equations (12),
- roots of the equations (12), ![]() - normalizing coefficients,
- normalizing coefficients,
![]() - orthonormalized basis of space
- orthonormalized basis of space ![]() .
.
Thus, spectral properties of the indignant operator of heat conductivity are investigated; Fourier submission of solutions of the mixed task for the heat conductivity equation is brought.
Results of article are an essential contribution to development of the general spectral theory of regional tasks for the differential equations.
The received results can be applied in further researches of regional tasks to the differential equations and theories of operators.
2. Elsgolts L.E., 1955, Qualitative methods in the mathematical analysis. GTTI, Moscow, 137-151.
3. Elsgolts L.E., and Norkin S. B., 1971, Introduction to the theory of the differential equations with the deviating argument. Science Publ., Moscow, 116-158.
4. Krasovsky N. N., 1959, Some tasks of the theory of stability of the movement. Fizmatlit Publ., Moscow.
5. Pinni E., 1961, Ordinary differential-difference equations. SILT Publ., Moscow, 88-107.
6. Bellman R., and Cook K.L., 1967, Differential-difference equations. World Publ., Moscow, 271-327.
7. Norkin S. B., 1965, The differential equations of the second order with the late argument. Some questions of the theory of fluctuations of systems with delay. Science Publ., Moscow, 301-318.
Rustemova K., Zhunisbekova D., Ashirbaev Kh., Dzhumagalieva A. ABOUT FOURIER OF REPRESENTATIONS THE SOLUTION OF THE MIXED TASK FOR THE HEAT CONDUCTIVITY EQUATION. International Journal Of Applied And Fundamental Research. – 2016. – № 5 –
URL: www.science-sd.com/467-25050 (30.01.2026).










 PDF
PDF