Meanwhile, quite recently it became obvious that couple of other, very different, objects and systems do possess this (or very similar) property. First of all, it concerns social systems [1]. Development process of particular group, ethnic group, state and humankind, in general, is defined by the past as well as by the present. Besides that, enormous number of non-living nature objects are discovered to have signs of memory. And this fact is no surprise, because, probably, it is difficult to define strict division between the objects of living and non-living character. It is rather artificial and vague [2].

Let's make as example of memory effects creation in physical macroscopic systems. We just mention Boltzman inheritage principle, which was mathematically developed Volterra in the end of XIX century [3].

Before that we're discussed macroscopic body of non-living nature. Nevertheless, as recent investigations are discovered, memory effects show up on microscopic (atomic and molecular) level. In principle we can talk of molecular memory. It's presence regulates some peculiarities of the progress of different irreversible processes, for example: magnetic, dielectric, structural relaxation, phenomena like viscosity, diffusion, thermoconductivity, etc.

During investigation and description of molecular memory effects most often terms of Markovian and non-Markovian random processes are used. Markovian process is characterized by the fact, that at given time t probability of magnitude of the variable doesn't depend on prehistory system development, but fully depend on the magnitude of the variable at present time. Processes, which post-influence effects are seen, are referred to non-Markovian as well. This incorporates with the fact that state of the system is defined by its whole evaluation from initial to final state.

The mathematical basis for constructing such equations was laid in the works Zwanzig [4] and Mori [5]. The developed procedure allows them to build for the study of the time correlation function a(t) an infinite chain of coupled non-Markovian kinetic equations of the following form

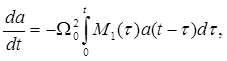(2)

...

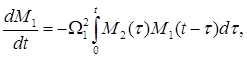Where -  i-th order memory functions, taking into account the effects of molecular memory.

The main problem with this approach is how to closure of an infinite chain of kinetic equations. For this purpose, the memory model functions, mode-coupling approximation of interacting modes, correlation and quasi-hydrodynamic approximation, as well as self-consistent approach generalizing some of them [6-10].

The results of the research allowed, in particular, to explain a number of different flow characteristics of irreversible processes: magnetic, dielectric, vibrational, structural relaxation, as well as phenomena such as viscosity, diffusion, thermal conductivity, and many others (see, for example, references in [11]).

Moreover, currently non-Markovian approach is becoming increasingly common, not only in physics but also in several other areas of human knowledge, such as chemistry, biology, medicine, geology, etc.

2. Ciolkovskij K.E. Monizm vselennoj. - Kaluga: izdanie avt., 1923. - 85s.

3. Volterra V. Theory of permutable function. - Princeton: Princeton University Press, 1915. - 66p.

4. Zwanzig R. Memory effects in irreversible thermodynamics // Physical Review. - 1961. - V.124, №5. - P.983-992.

5. Mori H. A continued fraction representation of the time-correlation function // Progress of Theoretical Physics. - 1965. - V.34, №3. - P.765-776.

6. Shurygin V.Yu., Yul`met`ev R.M. Influence of non-markov effects in the thermal motion of particles on the intensity of incoherent scattering of slow neutrons in a liquid // Theoretical and Mathematical Physics. - 1990. - V.83, №2. - P. 492-502.

7. Shurygin V.Yu., Yul`met`ev R.M. Spectrum of parameters characterizing the non-Markov behavior of relaxation processes in liquids // Sov. Phys. JETP, 1992. -V.75. - №3. – P. 466-471.

8. Yulmetyev R.M., Shurygin V.Yu., Yulmetyev T.R. Quasihydrodynamic approximation for memory functions in non-Markovian relaxation processes in condensed matter // Physica A. - 1997. - V. 242, № 3-4. - P. 509-521.

9. Yulmetyev R.M., Khusnutdinov N.R., Shurygin V.Yu. Transformation of non-Markovian kinetic equation for TCF to markovian type // Acta Physica Polonica B. - 1999. - V.30, №4. - P. 893-895.

10. Mokshin A.V. Self-consistent approach to the description of relaxation processes in classical multiparticle systems // Theoretical and Mathematical Physics. - 2015. - V.183, №1. - P. 449-477.