1. INTRODUCTION

Infectious disease such as Human immunodeficiency virus (HIV) and its consequences, Acquired immunodeficiency syndrome (AIDS), came of international recognition as far back as early 1980s [1] and have been adjudged the most deadly and global health disease of the 21st century with extra ordinary dimensions[2, 3]. Its transmission mode ranges from blood transfusion, vertical route intercourse, drug users, contaminated injecting equipment and commonly by heterosexual contacts [4].

In its complex and perilous nature of HIV/AIDS, there exists no known cure for the disease [5]. Prevention and suppression of HIV/AIDS are the possible means by which the spread of the disease can be control. Found promising in this direction, are barrier contraceptives (condom use) and the suppressing component – the antiretroviral therapy (ART). Other HIV/AIDS control measures are known to have emanated from mathematical models far back as 1987, when simple mathematical functions for the growth in the number of individuals who will ultimately develop AIDS and the distribution of incubation period of those individuals was developed [6]. More significant works on the dynamics and control measures of HIV/AIDS can be found in the studies [2, 3, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15].

In this paper, using mathematical model, we proposed a model which studies the dynamics of the impacts of heterosexual use of the condom in the presence of antiretroviral therapy (ART) for the prevention and possible eradication of the spread of HIV/AIDS. Related studies conducted were on the use of ART in the presence of counseling [11]; condom and ART were formulated with only the male population using the condom [2] and the model that studied the use of only condom (as a single treatment factor) by both male and female population [3].

Emphatically, the immense variation of this present model and any of the above highlighted studies lies in the natural birth rate of population understudy defined on mutual interactions between the male and female population (with only [2] accounting for this) and the fact that the present model explore the simultaneous use of the preventability measures (condom use and ART) by both infected male and female population, inclusive of condom use by their susceptible groups. Furthermore, the present model essentially focused on the impact of bi-therapeutic treatment of HIV/AIDS epidemic and the investigation of the outcome of possible variation on the application of treatment factors by both male and female population.

Section 2 accounts for the formulation of the model parameters and equations. Transformation of the model equations are carried out in section 3, followed by computer simulation in section 4. The last section is devoted to discussion of simulated results and conclusions.

2.1. THE MODEL PARAMETERS AND DIFFERENTIAL EQUATIONS

Here, we begin by initializing and defining the parameters which will be useful in structuring the differential flow-chart of the model.

Number of susceptible males at time t;

Number of infected males at time t;

Number of infected males who use both condom and ART at time t;

Number of susceptible males who use only condom at time t;

The rate of male infection at time t (incidence rate of males);

Average number of sexual contacts by infected male with females per unit time t;

Average number of sexual contact by infected males who use both condom and ART with females per unit time t;

Average number of sexual contact by susceptible males who use only condom with females per unit time t;

Probability of transmission by an infected male;

Probability of transmission by an infected male who use both condom and ART;

The proportion of infected males who use both condom and ART;

The proportion of susceptible males who use condom only;

Total population of males understudy;

where, .

Number of susceptible female at time t;

Number of infected females at time t;

Number of infected females who use both condom and ART at time t;

Number of susceptible females who use only condom at time t;

The rate of female infection at time t (incidence rate of females)

Average number of sexual contacts by infected female with males per unit time t;

Average number of sexual contact by infected females who use both condom and ART with males per unit time t;

Average number of sexual contact by susceptible females who use only condom with males per unit time t;

Probability of transmission by an infected female;

Probability of transmission by an infected female who use the condom and ART;

The proportion of infected females who use both condom and ART;

The proportion of susceptible females who use condom only;

Total number of female population understudy;

Where, .

Natural birth rate, ;

Natural death rate, ;

Related death rate of infected without treatment, ;

Related death rate of infected who use condom and ART;

AIDS-related death rate of susceptible male and female who use condom only;

Note: is negligible since susceptible with condom use may not transmit HIV.

The assumptions of this present model follow from those made by [2] with the following inclusions:

- Two treatment factors (condom use and ART).

- Both infected males and females use both condom and ART.

- Both susceptible males and females use condom only.

- Susceptible male and female that use condom only do not transmit infection

- AIDS-related death rate of susceptible population using condom is negligible.

From the above defined parameters and assumptions, we structure out the differential flow-chart (as in figure 1, below) which will be useful in formulating the model equations.

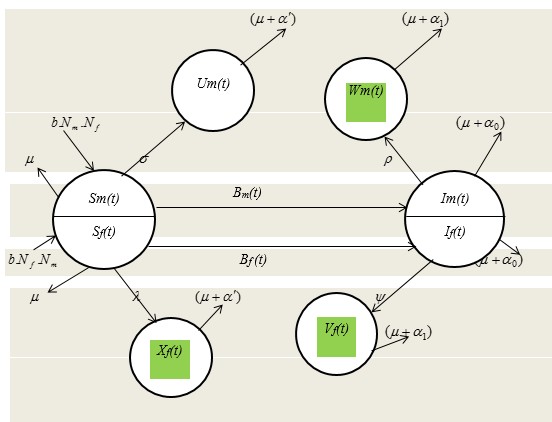
Figure 1: The differential flow-chart for the prevention of HIV/AIDS using condom and ART in a heterosexual population. Note: AIDS-related death rate is negligible

Employing fig.1 above, the model is governed by the following derived

differential equations:

(2.1)

(2.2)

(2.3)

= (2.4)

where, is negligible (period at which infection have not manifested).

Similarly, the female populations are derived as follows:

(2.5)

(2.6)

(2.7)

= (2.8)

Supplementing the differential equations, are algebraic equations of the population (male and female) understudy given as:

(2.9)

(2.10)

We define the incidence rate of infection and on the relationand of HIV infected individuals:

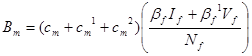(2.11)

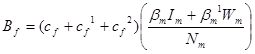(2.12)

2.2. EQUATION ANALYSIS

Analyzing equations (2.11) and (2.12), we see that in equation (2.11), if and from equation (2.12),, we obtain the incidence rate as in model [16]. If, and, we obtain the incidence rate as in model [5]. Looking deeply, from equations (2.4) and (2.8), if we let, then we return to the model by [11]. We also note that, model [3] investigated the awareness of condom use, employing statistical approach in its analysis, a method completely differing from our approach. Furthermore, equations (2.4) and (2.8) models the proportion of susceptible individuals who use only condom; and equations (2.11) and (2.12) model the infection rate of male and female population when the condom is not efficacious. Therefore, the clinical worthiness of this present model lies in these classical parameters.

3. EQUATION TRANSFORMATION

Necessary, is the transformation of the model equations into proportions of dimensionless quantities, a useful process which reduces complex equations to transmittable forms as well as initiating biological meanings and defining the prevalence rate of disease infection.

To achieve this, we let

,

So that

(3.1)

(3.2)

(3.3)

(3.4)

Then proportion wise, we have,

= (3.5)

Likewise,

(3.6)

(3.7)

(3.8)

(3.9)

and

= (3.10)

We as well, transform the incidence rate of infections and , as defined by equations (2.11) and (2.12) to dimensionless form:

i.e.

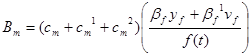(3.11)

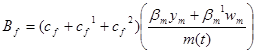(3.12)

Therefore, the progressions of infection are determined by the derived transformations of equations (2.1) – (2.4) and (2.5) – (2.8) respectively:

(3.13)

; (3.14)

; (3.15)

(3.16)

since, is negligible.

Likewise, equations (2.5) – (2.8) can be obtained as:

(3.17)

(3.18)

(3.19)

(3.20)

Hence, equations (3.13) – (3.20) can be represented in a simplified form as in table 1, below:

4. NUMERICAL EXPERIMENTS AND RESULTS

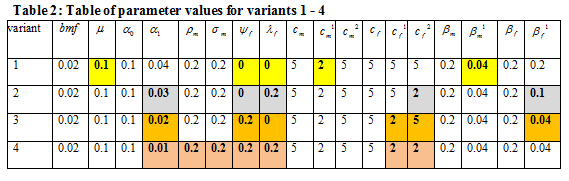
The model is investigated using the following numerical experiments (computer simulations) in a set of 8 nonlinear differential equations (as contained in table 1 above) in 8 different groups of the population. In the course of our investigation, we bear in mind that condom use by only susceptible males as well as condom use in the presence of ART by infected males had been studied in our previous models [2, 5]. So, we try as much as possible to keep these parameters constant. This task is accomplished with the aid of generated hypothetical values as given in table 2, below:

where the initial values of all characteristics 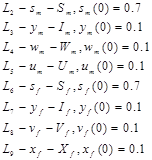are constant.

Here, we shall use the MATHCAD program, which is known for its in-built function “rkfixed” realizing Runge-Kutter method of accuracy of order 4 and then vector the parameters for compatibility.

Let

=

, .

Therefore, the systems of differential equations can be rewritten as:

.

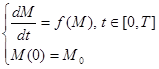Note: In each of figures (2 – 5), the investigations were carried out observing the highlighted parameters as in the corresponding variants (1 – 4) of table 2.

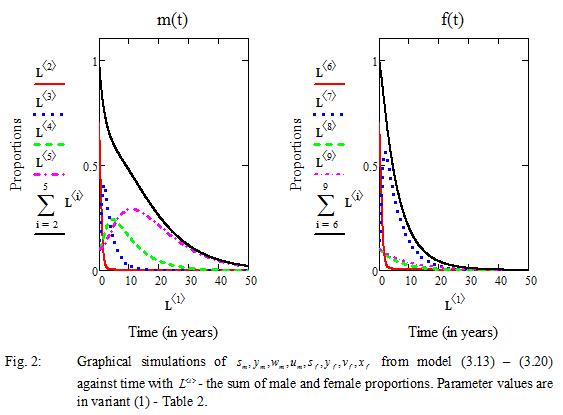
From figure 2 above, we investigate as in variant 1, table 2, the situation where only the males (susceptible and infected) use the condom as well as condom and ART simultaneously. Here, no female population uses any of the preventive measures (which serve as a control to our aim of investigation). With 10% natural death rate, low contact and transmission rate by the protected males proportions i.e., the observed numerical results were as follows: , and . This shows that the limit to which the entire population survives can be expressed by

and.

The implication is that, the entire male and female populations were contaminated with infection in less than 10 years. The susceptible population with condom use live a normal life and could survived for well over 50 years, while the infected with condom use and ART, live a prolonged lifespan of about 40 years. High level of infection for the unprotected females with the infected, living a maximum lifespan of 25 years, while the susceptible could survive for about 35 years.

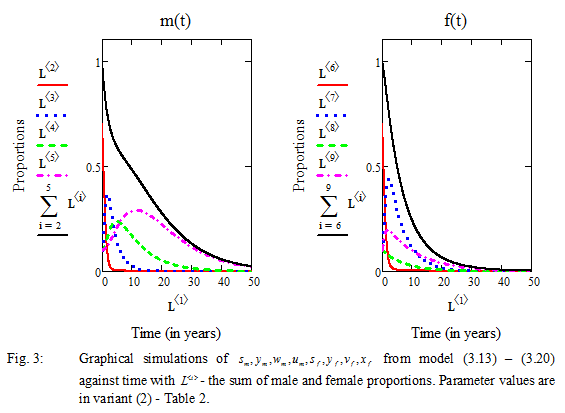
In figure 3 above, allowing the parameters as in variant 1, we carried out our investigation by varying only the following parameters (to obtain variant 2): . We obtained the following results for the various proportions: , and . The indication is that, the behavioral changes of the male population were similar to that of fig. 2, following their inert parameter values with slight increase in the years of the infected. The susceptible females with condom use survived a lifespan of about 40 years, suggesting the maximum lifespan of the female population.

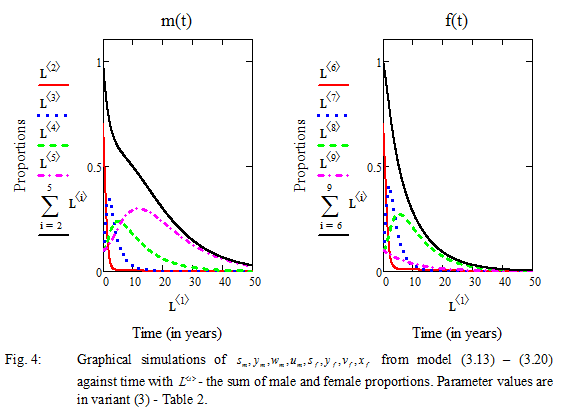
Furthermore, in figure 4 above, using parameters of variant 2, as the basis, we studied the impact of condom use in the presence of ART, by varying only the following parameters: (as contained in variant 3). We see that the male proportions exhibits a steady behavioral changes with only about 5 years decline in the lifespan of the infected without preventive measures. This is due to their interactions with the unprotected female proportion. On the other hand, the infected female with no condom use, had a maximum lifespan of 25 years, while the infected female proportion with two treatment factors ( condom use and ART), experienced decline in the number of infected population with survival length of about 40 years, indicating the lifespan of the entire population.

Finally in fig. 5 below, (from variant 4), we fortified our studies by regenerating the following parameters (i.e.). Here, susceptible males and females use the condom as well as simultaneous use of both condom and ART by the infected male and female proportions respectively, keeping rate of contact very low. Simulation indicates short lifespan of about 15 years by the infected males and females without preventive measures. The proportions of infected males and females that use both condom and ART live a more normal and prolonged lifespan. The susceptible male with condom use could be seen to survive well over 50 years while the female counterpart with decline in population survived for about 50 years.

5. DICUSSIONS

The present study had proposed a model, formulated via mathematical simulations. The model investigated the dynamical impact of heterosexual use of the condom in the presence of ART. Incorporated in the model, are the use of condom only by both susceptible male and female proportions; as well as the simultaneous use of both condom and ART by both infected male and female proportions. The model employed nonlinear differential equation represented by 8 different groups of the populations. In simulating, we involved the use of MATHCAD program (with in-built rkfixed function of Runge-Kutter order of accuracy 4).

Results obtained indicates that a lopsided preventive measures ( i.e. only the males use the prevention) have low significant impact in the eradication program, particularly on the part of the female population, as only the protected males survived over 50 years even with infection (see fig.2). On the other hand, the infected females without condom and ART remain infected with shorter lifespan of about 20 years. With inclusion of only the susceptible females that use the only the condom, the male population experienced a considerable reduction of infection resulting to slight increase in the number of years of survival. Clearly, the susceptible females with condom use survived for about 40 years as against a well over 50 years by their male counterparts. This variation suggests a probable low condom use by the female population. A study conducted by [3] – fig. 3.

Furthermore, we considered a reversion in the use of the preventive measures by the female population, where susceptible did not use the condom but the infected used the condom with ART (see figure 4). We observed some level of stability by the male population using the control measures with decline in the lifespan of infected due to interaction with infected females without condom use. The proportions of infected male and female population that use condom and ART live a normal and prolonged lifespan of about 40 years, while infected indicates a maximum of 25 years of survival.

In our final simulation, two treatment factors were comprehensively administered - the condom use (as single treatment) by both susceptible and condom use with ART (as combined treatment) by both infected male and female population. Prolonged and normal live of about 40 years were experience by the infected proportion with condom and ART, implying a reduction in the spread of HIV. Both infected males and females without preventive measures lived a shorter lifespan of 15 years. The susceptible male with condom use survived well over 50 years while the female counterpart with decline in population survived for about 50 years. This variation in years of survival can be attributed to the low application of condom use by the female population, which is in agreement with the studies by [3] – fig.5.

Generally, we see that the use of condom reduces spread of infection; adherent to use of ART, suppresses and slow the rate of infection while, the combination of condom use with ART will eradicate and prolong the lifespan of the infected in a considerable time interval.

6. CONCLUSION

The results of our computer simulations indicates that a possible control program of HIV/AIDS can be achieved where there is a persistent condom use by both susceptible males and females, as well as cogent combination of condom use and high significant adherent to ART by both infected male and female population. Also, a sufficiently high efficacy of condom use and reduced sexual contact rate would obviously enhance a more effective eradication program. The model therefore, recommend persistent and intensive awareness campaign; production of condom with the latest technology and effective use of preventability by both heterosexual population as means of achieving the goal of complete eradication of HIV/AIDS epidemic.

Acknowledgements

The two authors (Bassey, Echeng B., Lebedev, K. A), acknowledge with thanks, the support of the Department of Math and Computer Science, Kuban State University. We are also grateful to the reviewers (Prof. A. A. Halafian and Prof. H. M. Uranov) for their constructive comments, which have enhanced the paper.