In this work given a justification of the method of fictitious domains. For the first time obtained not improving mark of convergence rate of the solving the from auxiliary problem to solving the original problem at the time when the small parameter strive to zero.

The fictitious domain method is one of the known methods of approximate solutions of boundary value problems in mathematical physics. In general fictitious domain method is justified for the linear boundary value problems of mathematical physics. In this work is devoted to substantiation of the fictitious domain method for nonlinear elliptic equations. A new method of obtaining best possible rate of convergence of solutions in the method of fictitious domains .

Let's consider the boundary value problem for nonlinear elliptic equations in area with border area

, (1)

. (2)

As method of fictitious domains for the continuation of the lower coefficient in the auxiliary area with border Ø, solving equation with small parameter

, (3)

, (4)

where - continued with zero out of and

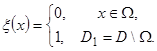
Next one notations used are from the monograph

Definition 2.1.1. Generalized solution of the exercises (3), (4) is the function , that is satisfying the integral identity

(5)

for all .

Theorem 1. Let’s . Then there exists a unique weak solution (3)-(4) and it is satisfied the estimate

(6)

where

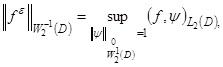
at that, when this solution converges to the generalized solution of the problem (1), (2).

Definition 2. Stronger solution of the problem (3)-(4) is called function , that satisfying to equation (3) almost everywhere.

Theorem 2.1.2. Let’s . Then there a stronger solution of the problem (3)-(4) and it is satisfied the estimate

, where at . (7)

Theorem 2. Let’s . Then

(8)

- positive constant that not depend from .

2. Смагулов Ш.С. Метод фиктивных областей для краевой задачи уравнений Навье-Стокса .- Новосибирск, 1979,(Предпринт/ВЦ СО АН СССР, №68.-С. 68-73.

3. Коновалов А.Н. Численные методы механики сплошной среды.-1972.-Т.3,№5. –С. 52-67.