About Us
Executive Editor:Publishing house "Academy of Natural History"
Editorial Board:
Asgarov S. (Azerbaijan), Alakbarov M. (Azerbaijan), Aliev Z. (Azerbaijan), Babayev N. (Uzbekistan), Chiladze G. (Georgia), Datskovsky I. (Israel), Garbuz I. (Moldova), Gleizer S. (Germany), Ershina A. (Kazakhstan), Kobzev D. (Switzerland), Kohl O. (Germany), Ktshanyan M. (Armenia), Lande D. (Ukraine), Ledvanov M. (Russia), Makats V. (Ukraine), Miletic L. (Serbia), Moskovkin V. (Ukraine), Murzagaliyeva A. (Kazakhstan), Novikov A. (Ukraine), Rahimov R. (Uzbekistan), Romanchuk A. (Ukraine), Shamshiev B. (Kyrgyzstan), Usheva M. (Bulgaria), Vasileva M. (Bulgar).
Materials of the conference "EDUCATION AND SCIENCE WITHOUT BORDERS"
Introduction
The quantitative prediction of restoration and age dynamics of forests is the central problem within the conception of the stable management of the resources. The aim of our research is to develop objective quantitative methods for the appreciation of the probability of dominant-forming species changing.
Material and methods
The area of the research is situated in the Zauralsky (Trans-Ural) hilly piedmont province (Middle Ural, Russia) between 57°00´–57°05´ N.lat. and 60°15´–60°25´ E.l. Restoration age dynamics from clear-cuttings (4-5 years old) up to tree stands of 65-160 years old has been studied. We previously have described the objects of research [2].
Results and discussion
We have built in the framework of the theory of catastrophes mathematical model of forest vegetation in clearings [1, 3]. This model allows us to construct potential functions:
![]() ,
, ![]() , (1)
, (1)
![]() ,
, ![]() . (2)
. (2)
Here ŋ = р0/рс–Тр0/рс – the parameter of the order characterizing the deviation of vegetation density (tree and grass) at the constant quantity of T, that is close to one, from some average meaning of pines and birches density of р0=(pp + pв)/2; ![]() ; rc – density scale; a*, b* – parameters: a*=–3(T2p0*–1), b*=–H*+3Tp0*–2T3p0*3. Parameter of b*=–H*+Hs* can be represented as a sum of the external field of H* and internal self-consistent Hs*=3Tp0*–2T3p0*3. H*=H/Hc, Hc – critical soil thickness. When b*=0, H*=Hs. F*=F/F0 – is the potential function of gathering catastrophe that defines energy characteristic in the cited form. Potential function for studied ecodynamic series are shown in fig. 1. System state stability is determined by their form. Availability of the local and global minimum in general case is determined with Thom theorem, in the case of gathering catastrophe – with non-zero values of the controlling parameter of b* (at b*=0 potential is symmetric). For two particular situations which we have observed, b* is different from 0: for cowberry shrub pine forests b*=-1.54*108; for grass-reed grass birch forests b*=-2.22*105. The difference between the examined pine forests and birch forests, by b* parameter makes up 3 orders.
; rc – density scale; a*, b* – parameters: a*=–3(T2p0*–1), b*=–H*+3Tp0*–2T3p0*3. Parameter of b*=–H*+Hs* can be represented as a sum of the external field of H* and internal self-consistent Hs*=3Tp0*–2T3p0*3. H*=H/Hc, Hc – critical soil thickness. When b*=0, H*=Hs. F*=F/F0 – is the potential function of gathering catastrophe that defines energy characteristic in the cited form. Potential function for studied ecodynamic series are shown in fig. 1. System state stability is determined by their form. Availability of the local and global minimum in general case is determined with Thom theorem, in the case of gathering catastrophe – with non-zero values of the controlling parameter of b* (at b*=0 potential is symmetric). For two particular situations which we have observed, b* is different from 0: for cowberry shrub pine forests b*=-1.54*108; for grass-reed grass birch forests b*=-2.22*105. The difference between the examined pine forests and birch forests, by b* parameter makes up 3 orders.
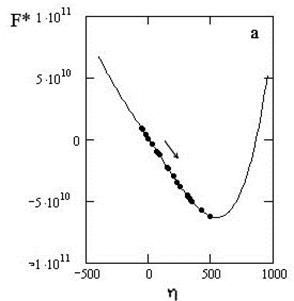
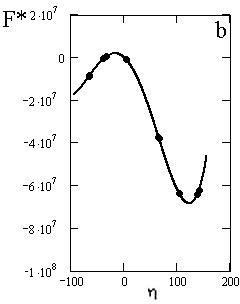
Fig. 1. Potential functions (points – empirical data, lines – the result of the equation solution (2)): а – cowberry shrub pine forests in the steep slopes of the southern exposition with small stony soils; б – grass-reed grass birch forests in the lower parts of gentle slopes with thick drained soils
We can judge the stability of the structure of the forest (the probability of changing edificator) based on the calculation of the distance from the separatrix (fig. 2). The equation of the separatrix of forest vegetation (а*/3)3+(b*/2)2= 0 characterize a limit to maintain dominance woody species (pine or birch) in the stand.
For cowberry shrub pine forests which we have studied (а*/3)3+(b*/2)2=5.92*1015, and for grass-reed grass birch forests (а*/3)3+(b*/2)2=–6.88*1010. These meanings show sufficient remoteness from separatrix both cowberry shrub pine forests and grass-reed grass birch forests. This is the evidence of the fact that the edificators change is unlikely.
The approach which we have suggested allows calculation susceptibility for the equation of ![]() (characteristic of the change of variable at the change of H* external field):
(characteristic of the change of variable at the change of H* external field):
![]() .
.
Under approaching the critical point ![]() , and the susceptibility tends to infinity. For cowberry shrub pine forests which we study the susceptibility amounts to 4.46*10-5, and grass-reed grass birch forests – 0.038.
, and the susceptibility tends to infinity. For cowberry shrub pine forests which we study the susceptibility amounts to 4.46*10-5, and grass-reed grass birch forests – 0.038.
Thus, objective quantitative methods of the estimation of stability of regeneration-age dynamics providing well-founded predicting of the condition of described objects were developed. As the main criteria of the stability of the development we suggest: remoteness from separatrix and the value of susceptibility.
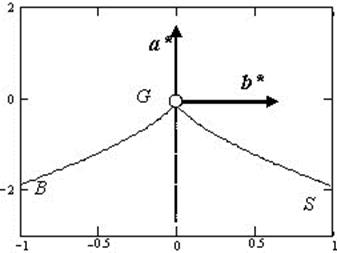
Fig. 2. BGS separatrix developing forest vegetation
Acknowledgments
The authors express sincere gratitude to doctors of physics-mathematics sciences, professor G.P. Bystrai for the methods and program product that he had granted.
2. Ivanova N.S., Zolotova E.S. Biodiversity of the natural forests in the Zauralsky hilly piedmont province// Modern problems of education and science (Sovremennye problemy nauki i obrazovanija). 2013.1. URL: http://www.science-education.ru/107-8563
3. Ivanova N.S., Zolotova E.S. Model of forest restoration // Population Dynamics: Analysis, Modeling, Forecast. 2013 (2). №2. P. 50-60.
Ivanova N.S METHODS OF THE ESTIMATION OF STABILITY OF REFORESTATION. International Journal Of Applied And Fundamental Research. – 2013. – № 2 –
URL: www.science-sd.com/455-24167 (12.03.2026).










 PDF
PDF