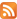Differential equations arise in many fi elds of application, such as in the simulation of phenomena in physics, mechanics, chemistry, biology and so forth. These equations are often in the form of a stiff initial value problems [1]-[3].

We describe a parallel explicit Runge- Kutta integration scheme second order in which an accuracy and stability control algorithm are included. The primary objective of this work is to illustrate a defi nite potential for the parallel performance.

Consider a stiff initial value problem

where y: [t0, tk] →RN,

f: [t0, tk] × RN → RN,

[t0, tk] – interval integration. Without loss of generality, assume that (1) is an autonomous system. Note that a non-autonomous system y´ = f(y, t) is always possible to write in an autonomous form as (1).

Assume that there exists a unique solution to the problem (1). Assume that p is an amount of processors on computational system, N is a dimension of the system (1) and N > p, we write a parallel explicit Runge-Kutta scheme as in [4]

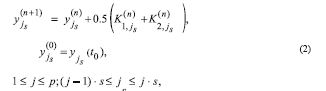
where s = N/p, if N multiple p, or [N/p] + g, otherwise,

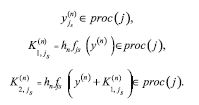
We design a parallel algorithm by using a graph reduction technique and decomposition technique on a subtasks [5], [6]. Our method based on the use of automatic control of accuracy and of stability dynamically as the solution develops. A value of a step size hn which will give the required solution with an estimated local error exactly equal to the requested tolerance and stability condition. The theoretical justifi cation for using variable stepsize algorithms to integrate stiff problems has been given in [1]. It is shown that when a variable stepsize of integration is used, the effi ciency of the explicit Runge -Kutta method can be increased by means of a step choosing algorithms in which an accuracy and stability are controlled. In our method, a stability control is based on using of a estimation of a largest eigenvalue of Jacobian matrix by a power method across of right side system (1) differential and the following control as h|λmax÷ ≤ D, where D is a stability region size. This approach leads not to increase in a calculation cost.

Parallel numerical algorithm is as follows. The , y are distributed onto a p of processes according to the block scheme to ensure «good» load balance as well as the scalability of the algorithm. An each task Uj is performed on one processor proc(j), Uj € proc(j). Proc(1) defi nes a value hn and broadcasts to the other proc(j), as operation one-to- all. An each proc(j) computes y ⁽ⁿ⁾ _js its part and broadcasts to the other proc(j), as all-to-all. In additional, proc(j) calculates a local norm, and sends to the proc(1).

The program code is written in C/C++ with MPI –functions. It is available from the authors. The computations were done on a cluster MVS ICM having 99 processors [7]. Some numerical results are presented to show the effi ciency of the parallel method. In additional, we give the number of integration steps, number of a function f evaluations, number of callbacks, i.e. isa, ifu and iwo, respectively.

References

1. Novikov E. Explicit methods for stiff systems. - Novosibirsk: Nauka. RAN, 1997.
2. Hairer E., Wanner G. Solving Ordinary Differential Equations II, Springer-Verlag, 1996.
3. Butcher J.C. Numerical Methods for Ordinary Differential Equations // John Wiley&Sons. - 2008.
4. Vashchenko G.V., Novikov E.A. Parallel implementation of explicit Runge-Kutta methods // Vestnik KrasGau. - 2010. - №2. - P. 14-18.
5. Quinn M.J. Parallel Programming in C with MPI and OpenMP. - New York, NY: McGraw-Hill, 2004.
6. Hendrickson B., Tamara G. Kolda Graph partitioning models for parallel computing // Parallel Computing. - 2002. - Vol. 26, № 12. - P. 181-197.
7. Isaev S.V., Malyshev A.V., Shаidurоv V.V. Development of the Krasnoyarsk´s parallel computing centre // Computing Technologies. -2006. - Vol. 11. - P. 28-33.