The conducting

Dispersing force in electromagnetic mechanoactivators(EMMA)is formed during the force interaction of the working organs of the apparatus in the magnetic liquefied layer created in the process of processing material under the influence of electromagnetic and mechanical forces [1,2,3,4].When passing through the elements of the EMMA magnetic flux, the grinding bodies are organized into various structural constructions and create magnetic liquefied layer which couples surfaceslimiting the volume of product processing [5,6].With a relative displacement of the surfaces, structural constructions are destroyed.In this case, the grinding bodies are informed of the kinetic energy of motion in the working volume of the apparatus.The process of purposeful reorientation of grinding elements in structural groups is accompanied by the creation of multipoint contact interactions between ferromagnatic elements and particles of processed product.Force action is manifested both in the form of compression forces, and shock-abrasive loads[7.8]. Physico-mathematical modeling of the process of formation of dispersive shock-abrasive loads between grinding ferromagnetic elementsthrough a layer of processed material and analysis of models a priori contributes to the design of energy-efficient EMMAwith various purposeswith high selectivity of dispersion [9, 10].

The goal:analysis of physical essenceof the process ofselective dispersion of materialswith various purposes in electromagnetic mechanoactivators.

Material and methods of research.The subject of research –the process of processing materials in the magnetic liquefied layer of ferromagnetic bodiesof electromagnetic mechanoactivators with the justification of the efficiency of selective dispersion.

The results of the study and their discussion. At present, there are two interpretations of the physical essence of the process of selective dispersion in mechanoactivators [1]:

- selectivity of grinding, when not all particles undergo a fracture under a single loading,

- selective grinding, when the formation of a new surface occurs along the boundaries of the intergrowth of the components.

The first interpretation is applied to the description of simple in composition materials, the second - for bulk polymorphic media.

By selectivity is meant a difference in the rate of formation of the new surface.

In this case, the analytical dependence for the degree of selective grinding has the form:

η= HG/(1 + HG), (1)

where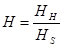—relative hardness byMoos (indeсesHand S correspond to more solid and softer components);

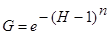— relative grinding of components;

n - empirical constant.

The main prerequisite for selective grinding is advisable to recommend the variability of the components of the dispersible material. Such data were obtained on the basis of analysis of the results of studies of the process of fatigue failure under the action of cyclically repeated loads with determination of fatigue limits for dispersible components. Such data were obtained on the basis of analysis of the results of studies of the process of fatigue failure under the action of cyclically repeated loads with determination of fatigue limits for dispersible components (studies have been carried out for the ranges of loads at which the process of destruction proceeds most selectively) [1, 3] .

The treatment of selective grinding as a process of formation of a new surface mainly along the edges of the intergrowth of phases is presented in the 1970s.by scientistsofResearch Institute «Mechanobr». The main task of grinding is recognized the need to destroy the multiphase product so as to maximize the release of the phases with their minimum destruction not allowing unwanted re-grinding, which contributes to increasing the energy intensity of the process. By the selective function, we mean the kinetic function of grinding a simple bulk material [3]. To determine the kinetic function of grinding, a stochastic approach is used.

The equation for determining the grinding speed has the form:

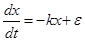, (2)

where x - particle size;

t - time;

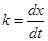—coefficient in the Kirpichev-Kick equation;

ε (t) - additive random component.

The rate of change in particle size is related to the specific work of destruction.

The selective function S (x)is determined by the formula:

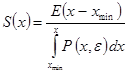, (3)

where Е— input energy;

x—average size of narrow loaded fraction;

xmin - the minimum particle size that can be formed by grinding;

ε - current particle size of the product of destruction;

Р(х, ε) - function characterizing the energy distribution by particles, the concrete form of which is determined by the corresponding law of destruction.

The expression (3) is distinguished by a greater universality than in (2), since it assumes the application of various energy laws depending on the conditions of grinding.

In studies, two-parameter measurements are also used:

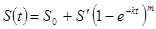(4)

where S(t) andS0 —current and initial values of the surface, respectively;

S’ —the maximum possible growth in the given conditions under given conditions;

k—empirical coefficient;

m— exponent that takes into account the imperfection of the process.

Thus, on the basis of the presented equations, we can proceed from the kinetic function of reducing the coarseness of simple materials with respect to composition to the selective function of the formation of a new surface along the interface of phase contact in materials that are complicated in structure. The process of destruction of the granular medium can be represented as stochastic Markovsky. The intensity of the transition λij of the system from the state Ci to the state Cj is the desired kinetic function of selective destruction. The assumption is because the state of a granular medium can be described by a function of its surface similarly to (4), and the intensity of the transition is the rate of formation of a new surface along the contact boundaries of the components in the particles.

If the area of the surface interaction of the components in the particles is taken as the defining parameter, then the expression for the selective function can be represented by the expression:

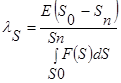, (5)

where Е —energy supplied to the material;

S0 andSn —initial and final total interaction surfaces of the components in the particles;

S—the current decreasing value of the phase contact surface;

F(S) —energy law as the most acceptable for the consideration of the process of formation of a new surface:

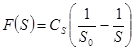, (6)

where Cs—a size coefficient of proportionality, showing the change in energy distribution with selective destruction in time, Joule / second.

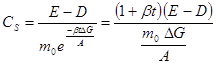, (7)

where D—dissipative energy losses in the working area of the chopper:

А —work of deformation and destruction of individual components; Then the initial number of particles;

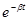—function to reduce the amount of unbroken particles in time;

β—empirical coefficient.

Expression (5) can be considered as a mathematical model that takes into account the most significant factors in a selective disintegration: kinetic energy E of working organs; The work of deformation and destruction of A of individual components entering into a complex body, as well as the strength of their interaction ΔG in the initial material; The main parameters of the granular medium, if the number of particles m0 is expressed in terms of the bulk density of pH and the volume of loading of the V material in the grinder.

The introduction of the exponential function in (7) was justified earlier by studies confirming its diminishing nature over time, which is explained by the increasing dissipation of energy in the granular medium and the increasing influence of the scale factor during grinding.The kinetic energy of the working bodies E can be determined by calculation, taking into account the material properties established by experimentally known methods of material testing.

Expression (5) is the base for mathematical modeling of processes and equipment for selective disintegration of multiphase bodies for various special purposes [1, 11, 12].

The conclusion

The results of the research presented in the article are the basis for developing a general theoretical approach to the creation of a new generation of energy-efficient devices for selective grinding of materials for various purposes.

2. Bezzubceva M.M., Volkov V.S. Mehanoaktivatoryagropromyshlennogokompleksa. Analiz, innovacii, izobretenija: monogorafija. - SPb.:SPbGAU, 2014. - 161 pp.

3. Bezzubceva M.M., Volkov V.S., Obuhov K.N.Nauchnoeobosnovanievnedrenijaimportozameshhajushhegosposobajelektromagnitnojmehanoaktivacii v apparaturno–tehnologicheskiesistemyshokoladnogoproizvodstva: monografija. – SPb.:SPbGAU, 2016. –197 pp.

4. BezzubcevaM.M.,VolkovV.S.Jenergokineticheskiezakonomernostijelektromagnitnojmehanoaktivacii: Monografija. SPb.:SPbGAU, 2016. 270 pp.

5. Bezzubceva M.M. Research of selective functions of grinding of chocolate mass in the electromagnetic mechanoactivation//International Journal Of Applied And Fundamental Research. – 2017. – № 1 – URL: www.science-sd.com/469-25205 (08.07.2017).

6. Bezzubtseva M.M., Volkov V.S. Approaches to the creation of energy efficient electromechanical devices for selective dispersion material //european journal of natural history. №3. – 2017. P. 52–55.

7. Bezzubtseva M.M., Volkov V.S. The issue research reliable operation of the with magnetic liquefaction layer //International journal of applied and fundamental research. – 2016. – № 1 – URL: www.science–sd.com/463–24972 (29.08.2016).

8. Bezzubceva M.M., Volkov V.S. To question the design of the model series electromagnetic mechanoactivation. // International journal of applied and fundamental research. – 2016. – № 3 – URL: www.science–sd.com/465–25007 (06.09.2016).

9. Bezzubceva M.M. ,Volkov V.S. A study of the power contacts in magnetic liquefied layer of ferro–impurities in the coolant in the working volume of electromagnetic densitometers (EPL)//A European journal of natural history. – №4. – 2016. P. 28–33.

10. Bezzubtzeva M.M., Volkov V.S., Gubarev V.N. The physical and mechanical processes study in ferro–bodies’ magneto – liquefied layer of electromagnetic mechano – activators (EMMA) . // International journal of applied and fundamental Research. – 2013. – № 2 – URL: www.science–sd.com/455–24425 (29.08.2016).

11. Bezzubceva M.M., Kotov A.V. Assessment of the magnetic fields structure in the working space of electromagnetic mechanical activators of cylindrical design. // International Journal Of Applied And Fundamental Research. – 2015. – № 1 – URL: www.science–sd.com/460–24756 (29.08.2016).

12. Bezzubceva M. M., Ruzhyev V.A., Yuldashev R. Z. Electromagnetic mechanoactivation of dry construc–tion mixes. // International Journal of applied and Fundamental Research. – 2013. – № 2 – URL: www.science–sd.com/455–24165 (16.11.2013).